PHASE (TRANSITIONS DE)

PHASE (TRANSITIONS DE)

Les premières transitions de phase observées ont été des changements d’état tels que la fusion de la glace ou la vaporisation de l’eau. Lors d’un changement d’état, le système, au sens de la thermodynamique, se présente comme la réunion de deux sous-systèmes homogènes possédant des propriétés distinctes. On appelle phase chacun de ces sous-systèmes. Plus précisément, une phase est une partie homogène, physiquement distincte, séparée des autres parties du système par une surface définie.

La phase sous laquelle un système se présente est déterminée par la connaissance d’un certain ensemble de paramètres intensifs: température, pression, champ électrique ou magnétique, etc. Si, pour diverses valeurs de ces paramètres, le système peut se présenter sous des phases différentes, il est possible d’observer le passage d’une phase à l’autre en modifiant continûment la valeur des paramètres intensifs. Dans ce cas, on dit qu’il y a changement de phase, ou transition de phase.

On distingue deux types de transitions: celles pour lesquelles, au point dit de transition, les deux phases, en présence l’une de l’autre, sont en équilibre, et celles pour lesquelles, au même point, on passe continûment d’une phase à l’autre, sans que les deux phases soient jamais en équilibre en présence l’une de l’autre. La fusion et la vaporisation sont des transitions du premier type. La grande majorité des transitions magnétiques, quelques transitions ordre-désordre dans les alliages et les transitions superfluide et supraconductrice sont du deuxième type. Les transitions de phase du premier type s’accompagnent toujours d’une discontinuité de l’entropie, ce qui se traduit par l’existence d’une chaleur latente de transformation. Les transitions de phase du deuxième type sont sans chaleur latente, mais présentent, en général, une anomalie de la chaleur spécifique au point de transition. P. Ehrenfest proposa, en 1933, d’appeler transitions du premier ordre les transitions s’accompagnant de discontinuités dans les grandeurs physiques, comme l’entropie, qui sont reliées à des dérivées premières de l’énergie libre, et transitions du deuxième ordre les transitions s’accompagnant de discontinuités dans les grandeurs physiques, comme la chaleur spécifique, qui sont reliées à des dérivées secondes de l’énergie libre, les dérivées premières étant continues.

Une notion très féconde pour classer les transitions fut introduite, en 1937, par L. D. Landau. Ce physicien remarqua que le passage d’une phase à l’autre, lors d’une transition du deuxième ordre, s’accompagnait d’un changement de symétrie, auquel il associa la notion de paramètre d’ordre. Cette grandeur, de caractère extensif, est nulle dans la phase la plus symétrique et non nulle dans l’autre. Ainsi, lors d’une transition paramagnétique-ferromagnétique, le paramètre d’ordre est l’aimantation, qui est nulle dans la phase paramagnétique et non nulle dans la phase ferromagnétique. La première, qui est isotrope, est plus symétrique que la phase ferromagnétique; dans cette dernière, il existe une direction privilégiée.

La théorie proposée par Landau est plus qu’une simple classification. À partir d’hypothèses qui semblent naturelles, telles que l’analyticité de l’énergie libre, elle permet de déterminer le comportement, au voisinage du point de transition, de diverses grandeurs thermodynamiques telles que le paramètre d’ordre, la susceptibilité, ou encore la chaleur spécifique. La théorie de la supraconductivité, dont on ignorait alors le mécanisme, que donnent, en 1950, L. D. Landau et V. L. Ginzburg est remarquable: elle postule que le paramètre d’ordre, caractérisant la transition à l’état supraconducteur, est un champ scalaire complexe «représentant une sorte de fonction d’ondes effective des électrons supraconducteurs».

Diverses études, tant théoriques qu’expériementales, devaient cependant montrer les limites de la théorie de Landau. La contradiction se manifeste pour la première fois, en 1944, lorsque L. Onsager montre que la chaleur spécifique du modèle d’Ising bidimensionnel n’est pas discontinue, mais présente une divergence logarithmique au point de transition. Dans les années 1960, un nombre considérable de travaux ont révélé que tous les systèmes physiques ne se comportent pas de façon identique au voisinage d’un point de transition et que, en outre, ces comportements, dit «critiques», sont plus singuliers que ceux qui étaient prévus par la théorie de Landau. Ces singularités sont caractérisées par des exposants critiques.

Les résultats les plus importants obtenus à l’époque furent la découverte des lois d’échelle, c’est-à-dire l’existence de relations entre les exposants critiques des diverses grandeurs physiques singulières d’un même système et celle de classe universelle, c’est-à-dire l’existence d’exposants critiques types déterminés par la symétrie du paramètre d’ordre et les dimensions du système.

Afin d’interpréter les lois d’échelle, B. Widom, en 1965, suppose que la partie singulière de l’énergie libre est une fonction homogène. Cette hypothèse, beaucoup moins restrictive que celle d’analyticité de Landau, permet, en particulier, de définir des variables réduites en fonction desquelles l’équation d’état, au voisinage d’un point de transition, prend une forme universelle; ce que l’expérience devait rapidement confirmer. Afin de justifier l’hypothèse de Widom, L. Kadanoff proposa en 1966 une nouvelle méthode d’étude du voisinage d’un point de transition. Kadanoff admet que si on divise le système en blocs dont les dimensions sont grandes par rapport à celles des objets microscopiques qui le constituent, mais petites par rapport à la portée des corrélations entre objets microscopiques, chaque bloc se comporte comme un objet unique. Cette hypothèse de similarité conduit, pour l’énergie libre du système, à la forme de Widom et entraîne, en outre, de nouvelles lois d’échelle.

Les travaux de Widom et Kadanoff provoquèrent un véritable raz-de-marée de publications, mais, jusqu’à la fin de 1971, les travaux théoriques ne firent que perfectionner quelques détails sans apporter de résultats vraiment nouveaux.

Au début de 1972, K. Wilson montre qu’il est possible d’exprimer certains exposants critiques sous la forme de séries de puissance de 﨎 = 4 漣 d , où d est la dimensionalité du système.

Ce développement, bien que surprenant à première vue, se comprend si on reprend le raisonnement, datant de 1960, de V. L. Ginzburg pour étudier le domaine de validité de la théorie de Landau. En introduisant la dimensionalité d du système, on trouve que, pour d supérieur à 4, les exposants critiques sont donnés par la théorie de Landau. Ce n’est que pour d inférieur à 4 que les exposants critiques prennent des valeurs différentes.

La théorie de Wilson est d’une importance considérable. Ses applications débordent le domaine des transitions de phase. Elle apparaît comme l’outil de choix pour l’étude des comportements singuliers en général.

Classification des transitions

Il est parfois possible de définir un paramètre d’ordre pour certaines transitions du premier ordre. C’est le cas de la transition paraélectrique-ferroélectrique du titanate de baryum, pour laquelle le paramètre d’ordre est la polarisation électrique. Mais on ne peut pas définir un tel paramètre pour les transitions entre deux formes cristallines différentes d’une même substance (polymorphisme) ou pour la vaporisation. Dans le premier cas, les symétries des deux phases sont différentes, mais on ne passe pas d’une phase à l’autre en perdant certains éléments de symétrie, ce qui est la condition nécessaire à la définition d’un paramètre d’ordre. Dans le second cas, les symétries des deux phases sont identiques et, là encore, il n’y a pas perte de certains éléments de symétrie quand on passe d’une phase à l’autre.

Les considérations de symétrie conduisent à distinguer deux types de transitions de phase suivant qu’il est possible ou non de définir un paramètre d’ordre.

En l’absence de paramètre d’ordre, deux éventualités peuvent se présenter: soit les groupes de symétrie des deux phases sont identiques (cas de la transition liquide-gaz), et ces transitions sont toujours du premier ordre au sens d’Ehrenfest; soit les groupes de symétrie des deux phases sont différents, mais aucun n’est un sous-groupe de l’autre (cas des transitions entre variétés polymorphes), et les transitions sont également du premier ordre au sens d’Ehrenfest.

Pour les transitions avec paramètre d’ordre, le groupe de symétrie de la phase la moins symétrique est un sous-groupe du groupe de symétrie de la phase la plus symétrique. On distingue, ici encore, deux cas: ou bien le paramètre d’ordre, en tant que fonction de la température, est discontinu au point de transition (cas de la transition ferroélectrique du titanate de baryum), et la transition est du premier ordre au sens d’Ehrenfest; ou bien le paramètre d’ordre est une fonction continue de la température au point de transition, et les transitions de ce type sont du deuxième ordre, bien que les anomalies de chaleur spécifique, par exemple, ne soient pas toujours du type imaginé par Ehrenfest.

Transitions sans paramètre d’ordre

Les transitions sans paramètre d’ordre, comme toutes celles du premier ordre, sont caractérisées par le fait qu’au point de transition les deux phases en présence sont en équilibre.

Changements d’état

Les transitions sont souvent sensibles à diverses actions extérieures. La température de vaporisation, par exemple, est sensible à la pression. Dans un diagramme (p , T), le lieu des points de transition liquide-gaz constitue la courbe de vaporisation. Dans le même diagramme, on définit de façon analogue la courbe de fusion et de sublimation. Ces trois courbes ont un point commun, le point triple, pour lequel les trois phases (solide, liquide et gazeuse) sont en équilibre. Pour toutes les transitions du premier ordre, il est possible de déterminer une chaleur latente de transformation. Dans le cas de la fusion, de la vaporisation ou de la sublimation, la chaleur latente L est liée à la variation du volume spécifique V lors du passage d’une phase à l’autre, et à la pente dp /d T de la ligne de transition par la formule de Clapeyron:

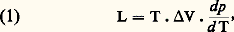où T désigne la température absolue au point de transition. La démonstration de cette formule s’effectue en écrivant que les deux phases en présence sont en équilibre thermodynamique en deux points de transition voisins.

Cette formule a de très nombreuses applications, dont celle de prévoir dans quel sens varie la température de fusion avec la pression. La fusion s’accompagne toujours d’une absorption de chaleur; en outre, dans la plupart des cas, le solide a un volume spécifique plus faible que le liquide: il s’ensuit que dp /d T est positif, et la température de fusion augmente avec la pression. Le cas de l’eau est particulier, car, la glace étant moins dense qu’elle, la température de fusion diminue quand la pression augmente. La formule de Clapeyron permet aussi d’estimer approximativement la pente de la courbe de vaporisation si l’on suppose négligeable le volume spécifique du liquide en comparaison de celui de la vapeur et si on assimile la vapeur à un gaz parfait. Pour une mole, on remplace donc V par RT/p et l’on obtient:

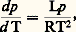où R est la constante des gaz parfaits.

On a réussi à suivre des courbes de fusion jusqu’à des pressions de l’ordre de 3 憐 10⁹ Pa et jusqu’à des températures de quelques centaines de degrés. Ces expériences ont révélé que la courbe de fusion semble se prolonger indéfiniment, contrairement à la courbe de vaporisation qui est limitée par le point critique (fig. 1). Si l’on peut passer continûment de l’état gazeux à l’état liquide, il est impossible de passer sans discontinuité de l’état liquide à l’état solide. L’état gazeux et l’état liquide sont qualitativement identiques, car ils sont tous deux isotropes, tandis que l’état solide cristallisé est anisotrope.

Polymorphisme cristallin

Les transitions entre variétés cristallines différentes d’un même corps pur sont, elles aussi, des transitions sans paramètre d’ordre. À une température et à une pression déterminées, la phase la plus stable est celle dont le potentiel thermodynamique est le plus bas. La variation de volume qui accompagne une transition entre deux formes cristallines différentes étant, en général, très faible, on peut la négliger et discuter la stabilité des diverses phases à l’aide de l’énergie libre F. Les exemples de polymorphisme sont très nombreux. Plus de la moitié des corps simples possèdent cette propriété. Les cristaux de soufre, obtenus à froid par évaporation d’une solution dans le sulfure de carbone, sont orthorhombiques, tandis que ceux qui se forment par refroidissement du soufre liquide sont monocliniques. L’étain blanc quadratique, stable au-dessus de 18 ⁰C, se transforme au contact d’un germe en étain gris cubique au-dessous de cette température. Le fer a un comportement un peu particulier qu’explique la figure 2. Cubique centré à température ordinaire, il devient cubique à faces centrées à 910 ⁰C et redevient cubique centré au-dessus de 1 390 ⁰C. La formule de Clapeyron est aussi applicable aux transitions entre les différentes formes cristallines d’un même corps pur. Soit le cas du soufre dont le diagramme de phase est représenté sur la figure 3. Sous la pression atmosphérique, les cristaux orthorhombiques, stables à basse température, se transforment, à 95,4 ⁰C, en cristaux monocliniques avec absorption de chaleur et augmentation de volume. La température de transition doit donc être une fonction croissante de la pression. L’expérience confirme cette prévision, car la température de transition augmente de 0,05 ⁰C par bar (1 bar = 10⁵ pascals). Au-dessus du point triple T, les cristaux orthorhombiques fondent sans passer par la phase monoclinique intermédiaire. Les transitions entre phases solides ne s’effectuent que si on les amorce par un germe cristallin. Si, sous la pression atmosphérique, on chauffe du soufre orthorhombique à l’abri de germes monocliniques, on peut le fondre à 114 ⁰C. La ligne en pointillé BT de la figure est la courbe de fusion de la variété orthorhombique. Dans la région ATB, cette variété peut exister, mais elle est métastable, c’est-à-dire moins stable que la variété monoclinique. De façon analogue, dans la région BTC, c’est le liquide qui est métastable. L’existence d’un retard à la transformation d’une phase en une autre et l’observation de phases métastables sont caractéristiques des transitions du premier ordre. La métastabilité a parfois un intérêt pratique, comme dans le cas de l’étain. Au-dessous de 18 ⁰C, l’étain blanc est métastable et, en présence d’un germe, il se transforme en étain gris pulvérulent. En hiver, les objets en étain risquent donc d’«attraper la peste de l’étain» et de tomber en poussière. Ce phénomène est toutefois très rare, car les germes qui peuvent l’amorcer n’existent pas en général. Il peut cependant y avoir production spontanée de germes, qui n’est appréciable qu’aux environs de 漣 50 ⁰C, alors que la vitesse de transformation est maximale vers 0 ⁰C. Ces résultats expliquent pourquoi la peste de l’étain ne peut s’observer qu’après des hivers particulièrement rigoureux; les germes produits lors des grands froids provoquent la transformation lorsque la température remonte aux environs de 0 ⁰C.

Transitions avec paramètre d’ordre

Recherche des paramètres d’ordre

Pour pouvoir définir un paramètre d’ordre, il faut que, lors de la transition, le passage d’une phase à l’autre s’accompagne de la perte de certains éléments de symétrie. Dans le cas déjà cité de la transition paramagnétique-ferromagnétique, l’aimantation joue le rôle de paramètre d’ordre. Pour les alliages, dans la phase désordonnée, certains sites de la structure sont équivalents. Permuter entre eux deux atomes occupant deux sites équivalents ne modifie en rien la structure. Les sites sont indiscernables. Le groupe de symétrie de la phase désordonnée est un groupe de permutations. Dans la phase ordonnée, les sites ne sont plus tous équivalents, certains étant occupés préférentiellement par un type d’atome. Le groupe de symétrie de la phase ordonnée comporte donc moins d’éléments. On dit que la transition de phase brise la symétrie de la phase désordonnée. La modification de la symétrie apparaît dès que se manifeste la plus légère occupation préférentielle de certains sites. Soit, plus précisément, un alliage dont la structure désordonnée comporte, comme dans le laiton 廓, deux types de sites équivalents. Le groupe de symétrie de cette phase n’a que deux éléments: la permutation identique, qui laisse les sites inchangés, et la permutation qui échange les deux sites. Pour définir un état du système, on peut se donner les proportions n ¹ et n ² des deux types d’atomes occupant l’un des réseaux. Si, à la température T, l’alliage est en équilibre thermodynamique, les valeurs de n ¹ et de n ² sont telles que l’énergie libre F(T; n ¹, n ²) est minimale. En tant que fonction de n ¹ et de n ², F est invariante par permutation de n ¹ et de n ². On a donc:

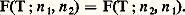Pour étudier les propriétés de symétrie de F, les variables n ¹ et n ² ne sont pas les plus appropriées. Les variables 益 et 兀, définies par:

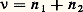et:

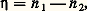sont préférables, car, lorsqu’on permute n ¹ et n ², 益 ne change pas et 兀 ne fait que changer de signe. Dans la phase désordonnée, toute fonction de n ¹ et de n ² qui n’est pas invariante par permutation est nécessairement nulle. 兀 est donc nul dans la phase désordonnée. Dans la phase ordonnée, il n’y a plus invariance par permutation et 兀 n’est pas nul: c’est le paramètre d’ordre de la transition ordre-désordre considérée; 益 ne peut pas être un paramètre d’ordre, car, étant invariant par permutation, il n’a aucune raison d’être nul dans la phase désordonnée; 益 et 兀 possèdent une propriété importante qui permet de les déterminer. Étant donné la forme quadratique symétrique en n ¹ et en n ² la plus générale:

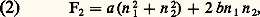elle s’écrit, en fonction de 益 et de 兀, sous la forme d’une somme de carrés:

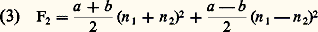ou: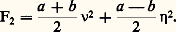

Cette transformation permet la recherche des paramètres d’ordre, une fois les variables choisies. La forme quadratique la plus générale (formule 2) est invariante par toutes les opérations de symétrie de la phase la plus symétrique qui, par extension, est appelée phase désordonnée quelle que soit la nature de la transition. Les nouvelles variables ainsi définies sont des paramètres d’ordre possibles si elles ne sont pas invariantes par toutes les opérations de symétrie de la phase désordonnée. Un paramètre d’ordre est toutefois invariant par certaines opérations de symétrie. Celles-ci constituent le groupe de symétrie de la phase ordonnée.

Le paramètre d’ordre qui décrit la transition ordre-désordre d’un alliage est un scalaire. Cependant, la nature mathématique du paramètre d’ordre n’est pas toujours aussi simple et sa détermination demande une analyse des propriétés de symétrie de la phase désordonnée, ainsi que celles des objets constituant le système. Par exemple, de nombreuses substances organiques passent de l’état liquide à l’état solide par une série de phases intermédiaires. Ces mésophases ont été baptisées cristaux liquides, car elles allient la fluidité du liquide à l’anisotropie du cristal. Elles possèdent une riche diversité de structures et des propriétés physiques intéressantes ^{[cf. CRISTAUX LIQUIDES]}. Les substances qui présentent des phases de ce type sont, en général, constituées de longues molécules en forme de barreau ou de latte. C’est le cas du para-azoxyanisole qui, entre 116 ⁰C et 136 ⁰C, est dans l’état nématique. Les grands axes des molécules, orientés au hasard dans la phase liquide ordinaire, sont, dans l’état nématique, parallèles entre eux, mais les centres de gravité des molécules sont distribués au hasard. La transition liquide ordinaire-état nématique brise la symétrie de la phase isotrope, laquelle est invariante par rotation dans l’espace tridimensionnel. La transition de phase paraferromagnétique, caractérisée par un paramètre d’ordre vectoriel, l’aimantation, brise aussi la symétrie de rotation de la phase paramagnétique, dans laquelle aucune orientation n’est privilégiée; cependant, la phase ferromagnétique a une symétrie différente de la phase nématique. La première a les mêmes éléments de symétrie qu’un cylindre de révolution (il y a un axe de rotation, mais aucune des deux directions de l’axe n’est privilégiée), alors que la seconde a la symétrie d’un cône de révolution (une des deux directions, celle dans laquelle pointe l’aimantation, est privilégiée). Le paramètre d’ordre de la phase nématique est un tenseur irréductible de rang 2.

Théorie de Landau

À la température T, l’état d’équilibre stable, caractérisé par une valeur 兀 du paramètre d’ordre, est tel que l’énergie libre F(T; 兀) est minimale. Soit ⁰ la température de transition. Si l’on suppose que la phase ordonnée est stable à basse température, on doit avoir 兀 令 0 si T 礪 ⁰ et 兀 0 si T 麗 ⁰. Si la transition est du deuxième ordre, on peut développer F(T; 兀) en une série de puissances de 兀 au voisinage de ⁰:

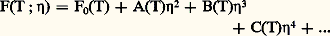Si T est supérieur à ⁰, l’énergie libre est minimale pour 兀 = 0; le développement précédent ne comporte pas de terme du premier degré en 兀 et A(T) doit être positif. Si, au contraire, T est inférieur à ⁰, l’énergie libre doit être minimale pour une valeur de 兀 différente de zéro et A(T) doit être négatif. Au point de transition, A(T) doit donc s’annuler. La fonction A(T) la plus simple qui satisfait à toutes ces conditions est:

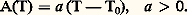Pour que le point de transition soit lui-même stable, il faut que F(T⁰; 兀) soit minimale pour 兀 = 0, ce qui impose:

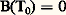et: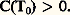

Il serait fortuit qu’au point de transition A(T) et B(T) s’annulent simultanément; aussi Landau suppose que B(T) est identiquement nul. En outre, C(T) étant positif pour T = ⁰, il reste positif si l’on ne s’écarte pas trop de ⁰; il est donc légitime de remplacer C(T) par une constante c positive. Dans ces conditions, on a:

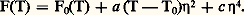La valeur de 兀 qui rend cette expression minimale est une solution de l’équation:

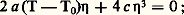celle-ci n’a qu’une solution réelle, 兀 = 0 si T 礪 ⁰, tandis qu’elle en a trois, 兀 = 0 et 兀 = 梁 連a (T⁰ 漣 T)/2c si T 麗 ⁰. Dans ce dernier cas, la solution 兀 = 0 est à rejeter, car elle correspond à un maximum de F(T; 兀), c’est-à-dire à un équilibre instable. La théorie de Landau implique donc, pour le paramètre d’ordre 兀, un comportement en 連⁰ 漣 T, avec ⁰ 礪 T, au voisinage de ⁰. L’expression de l’énergie libre adoptée par Landau permet de calculer la capacité thermique massique et la susceptibilité relative au paramètre d’ordre au voisinage de la température de transition. On trouve que la capacité thermique massique est discontinue au point ⁰ et que sa valeur dans la phase ordonnée est supérieure à sa valeur dans la phase désordonnée au voisinage de ⁰. Quant à la susceptibilité isotherme relative au paramètre d’ordre, elle se comporte comme 1/|T 漣 ⁰| au voisinage de ⁰.

Ce dernier résultat avait déjà été obtenu, dès 1906, par P. Weiss dans le cas d’une transition paraferromagnétique. Le raisonnement de Weiss est particulièrement simple. En 1905, P. Langevin, en supposant qu’un corps paramagnétique est constitué de petits aimants sans interaction entre eux, avait montré que, à température suffisamment élevée, l’aimantation M a pour expression:

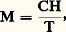où H est le champ magnétique appliqué, T la température et C la constante de Curie.

Cette formule était en excellent accord avec les résultats expérimentaux obtenus par P. Curie dans sa thèse soutenue en 1895. Reprenant la théorie de Langevin, Weiss prend en compte les interactions entre aimants élémentaires, en supposant que chacun d’entre eux est soumis à un «champ moléculaire» H^m , s’ajoutant au champ extérieur H, créé par l’ensemble des autres petits aimants. En outre, Weiss suppose que H^m est proportionnel à l’aimantation M. Il suffit alors de remplacer, dans la formule de Langevin, H par H + KM, où K est une constante, pour aboutir au résultat M = CH/(T 漣 ⁰) où ⁰ = CK.

La démarche de P. Weiss, qui par la suite a été généralisée et appliquée à l’étude de nombreuses transitions de phase, était déjà en germe dans les travaux de Van der Waals qui, pour établir l’équation d’état des fluides qui porte son nom, tenait compte de l’interaction entre molécules par un terme de pression intérieure analogue au champ moléculaire.

En conclusion, l’expérience ne confirme pas, dans la plupart des cas, les résultats de la théorie de Landau. La raison en est que l’énergie libre, en tant que fonction de 兀, est certainement singulière au voisinage du point de transition et que, par conséquent, le développement en puissances de 兀 n’a pas de sens. La théorie de Landau suppose aussi que le paramètre d’ordre a la même valeur en tout point du système. Cette hypothèse est d’autant plus fausse qu’on est près du point de transition. En réalité, le paramètre d’ordre fluctue autour d’une valeur moyenne; loin du point de transition, les fluctuations peuvent être négligées, mais il n’en est pas de même au voisinage immédiat de ce point.

Phénomènes critiques

Après 1960, les très nombreux travaux consacrés à l’étude des phénomènes critiques ont révélé l’existence de ressemblances frappantes dans le comportement de systèmes physiques très différents. L’essentiel à retenir des résultats expérimentaux obtenus est que les comportements du paramètre d’ordre, de la capacité thermique massique et de la susceptibilité relatives au paramètre d’ordre sont, sauf dans le cas des supraconducteurs, très différents des comportements prévus par la théorie de Landau. Cela met en évidence le rôle fondamental des fluctuations du paramètre d’ordre.

Les exposants critiques

Afin d’étudier le comportement des grandeurs physiques singulières au voisinage d’un point de transition du deuxième ordre, on a pris l’habitude de les représenter par une puissance de |⁰ 漣 T|. Chaque grandeur est ainsi caractérisée par un exposant critique . Si h désigne le paramètre intensif conjugué du paramètre d’ordre, suivant une nomenclature introduite par M. E. Fisher, on pose, pour la capacité thermique massique à h constant, respectivement si T 礪 ⁰ et si T 麗 ⁰:

pour le paramètre d’ordre, si h = 0: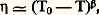

pour la susceptibilité isotherme relative au paramètre d’ordre, respectivement pour T 礪 ⁰ et pour T 麗 ⁰:

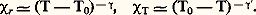Ces divers exposants ne sont pas indépendants. On a, par exemple, l’inégalité (G. S. Rushbrooke):

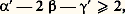qui est une conséquence immédiate de la relation thermodynamique:

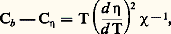simple transposition de la formule classique donnant C^p 漣 C^v. En 1963, J. W. Essam et M. E. Fisher ont suggéré que l’inégalité devait en fait être une égalité.

Bernard Widom réussit à établir cette relation en formulant l’hypothèse qu’au voisinage d’un point de transition du deuxième ordre la partie singulière de l’énergie libre (c’est-à-dire celle qui détermine les exposants critiques) est donnée par:

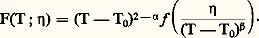La partie singulière de l’énergie libre est donc une fonction homogène généralisée de l’écart de température T 漣 ⁰ et du paramètre d’ordre 兀. Elle ne dépend que de deux exposants 見 et 廓, choisis de façon à ce qu’ils coïncident avec les exposants critiques de même nom. La relation d’Essam et Fisher s’obtient en dérivant deux fois F en 兀. En effet:

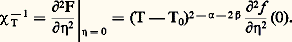Or:

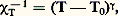d’où: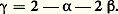

L’hypothèse d’homogénéité de F(T; 兀) a permis à Widom d’établir d’autres relations, par exemple,

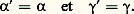Ces résultats ont suscité un grand nombre de travaux. En particulier, les physiciens ont étudié systématiquement différents modèles et, grâce au développement de l’informatique, ils ont réussi à déterminer leur comportement critique.

Les différents modèles

La théorie rigoureuse d’une transition particulière, dans le cadre de la mécanique statistique, soulève d’énormes difficultés mathématiques. Ces difficultés ont incité les théoriciens des phénomènes critiques à imaginer des modèles suffisamment simples pour faciliter les calculs. Citons:

– Les solutions solides binaires avec interactions limitées aux premiers voisins.

– Le modèle de fluide de Yang et Lee. Ces derniers supposent que les atomes d’un type donné ne peuvent occuper dans l’espace que les nœuds d’un réseau. La densité est proportionnelle au nombre de sites occupés et, l’énergie de configuration étant seule prise en compte, l’énergie cinétique est ignorée. Malgré son caractère assez grossier, ce modèle permet de rendre compte de la transition liquide-gaz de façon qualitativement satisfaisante.

– Le modèle d’Ising. Proposé en 1925 pour tenter d’interpréter la transition paramagnétique-ferromagnétique, ce modèle suppose que chaque nœud du réseau est occupé par un atome porteur d’un moment magnétique qui ne peut s’orienter que parallèlement ou antiparallèlement à un champ magnétique extérieur. Les interactions entre moments magnétiques sont limitées aux premiers voisins.

– Le modèle n -vectoriel. C’est la généralisation du précédent. Ici chaque nœud du réseau est occupé par un vecteur de longueur unité ayant n composantes. L’interaction entre deux vecteurs voisins ひ¹ et ひ² est de la forme 漣 J ひ¹ . ひ² où J est une constante positive. Le modèle d’Ising correspond à n = 1.

– Le modèle de Potts. C’est encore une généralisation du modèle d’Ising. Chaque nœud du réseau est occupé par un objet qui peut être dans q états différents. L’interaction entre deux objets voisins est égale à 漣 J ou 0, suivant que ceux-ci sont dans le même état ou dans des états différents. À un changement d’échelle d’énergie près, le modèle d’Ising correspond à q = 2.

L’intérêt de ces divers modèles déborde l’étude des transitions de phases ordinaires. Les polymères, par exemple le polyéthylène ou le polystyrène, sont des molécules organiques constituées d’un nombre N très grand de monomères identiques. La longueur, bout à bout, des chaînes de polymères en solution diluée est aléatoire. On trouve que la racine carrée de la moyenne quadratique de ces longueurs varie comme N size=1^益, où 益 est un exposant universel qui vaut environ 3/5. C’est l’analogue d’un exposant critique rencontré dans la théorie des changements de phase. Ce résultat n’est pas qu’une simple analogie. P. G. de Gennes a démontré, en 1972, que les exposants critiques des polymères se confondaient avec ceux du modèle n -vectoriel, dans la limite n = 0.

– Le modèle de percolation. L’étude d’un grand nombre d’objets qui peuvent se connecter est décrite par le modèle dit de percolation ^{[cf. PERCOLATION]}. Considérons un réseau cubique dans lequel les liaisons entre deux sites voisins sont formées de façon aléatoire avec la probabilité p . On appelle amas un ensemble de sites connectés par des liaisons. Pour une valeur de la probabilité p ^c , dite seuil de percolation, il apparaît un amas géant s’étendant d’un bord à l’autre du réseau. Si p 麗 p ^c , tous les amas sont de taille finie. Dans la limite d’un réseau infini, la taille de l’amas géant, au voisinage de p ^c , croît comme:

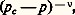où 益 est un exposant critique universel qui vaut environ 0,88.

On démontre que les exposants critiques du modèle de percolation sont ceux du modèle de Potts, dans la limite q = 1.

Résultats théoriques et expérimentaux

Le problème posé par le modèle d’Ising a été étudié par son auteur dans le cas d’un réseau à une dimension. Ce système ne présente aucune transition, ou, plus exactement, sa température de transition est nulle, ce qui signifie que le réseau unidimensionnel est ordonné à 0 K et désordonné à toute température non nulle. La solution du problème d’Ising, dans le cas d’un réseau carré à deux dimensions, a été trouvée en 1944 par L. Onsager. Cette solution, compliquée, a été par la suite simplifiée et complétée par certains auteurs. Sans entrer dans les détails, on se contentera ici d’indiquer quelques résultats:

– À la température de transition, la chaleur spécifique diverge de façon logarithmique ( 見 = 見 = + 0, la notation + 0 signifiant infiniment petit et positif).

– Au voisinage de la température de transition, le paramètre d’ordre se comporte comme |⁰ 漣 T|^1/8.

– Au voisinage de la température de transition, la susceptibilité relative au paramètre d’ordre se comporte comme |⁰ 漣 T| size=1^漣7/4.

On notera que ces résultats sont en parfait accord avec les deux relations de Widom ainsi qu’avec celle d’Essam et Fisher.

Tous les essais en vue de résoudre le problème d’Ising, dans le cas d’un réseau tridimensionnel, n’ont pas, jusqu’à présent, été couronnés de succès. Cela est regrettable, car les résultats sont très affectés par le nombre de dimensions du système. Diverses techniques d’approximations successives ont permis, toutefois, d’estimer les exposants critiques. G. A. Baker et D. S. Gaunt ont publié, en 1967, les résultats suivants:

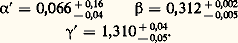Ici encore, on constate que la relation d’Essam et Fisher est satisfaite.

Pour le modèle n -vectoriel, E. Stanley a obtenu en 1971, dans le cas d’un réseau tridimensionnel, les résultats suivants:

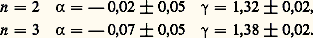Il apparaît que, pour la classe de modèles considérés (interaction de la forme ひ¹ . ひ²), les exposants critiques ne dépendent que de la dimension de l’espace et du nombre de composantes n du paramètre d’ordre. Ils sont indépendants de la portée des interactions, de la géométrie du réseau, du caractère quantique ou classique des objets qui s’ordonnent, etc. Cette propriété constitue ce qu’on appelle l’«universalité».

Les résultats expérimentaux confirment cette propriété. Il faut toutefois souligner que l’interprétation des expériences est extrêmement délicate et il est fréquent que les résultats diffèrent d’un expérimentateur à l’autre. Les valeurs des exposants critiques sont facilement altérées, d’une part, par une modification, même légère, de la température de transition, laquelle n’est pas toujours parfaitement définie, et, d’autre part, par le choix du domaine de température |T 漣 ⁰|⁰ autour du point de transition, dans lequel on représente le comportement de la grandeur physique singulière par un exposant critique.

Groupe de renormalisation

La théorie des phénomènes critiques a fait un progrès décisif avec la publication en 1972 par K. Wilson d’une nouvelle méthode de calcul des exposants critiques. Au voisinage du point de transition, la longueur de corrélation entre, par exemple, les moments magnétiques d’un cristal ferromagnétique devient très grande. Le problème devient donc compliqué puisque, compte tenu de l’importance du nombre de moments magnétiques corrélés, le nombre de degrés de liberté du système est élevé. Suivant une idée de Kadanoff, on peut simplifier ce problème en considérant un système pour lequel la longueur de corrélation est beaucoup plus petite. On divise pour cela le réseau en blocs. Dans chaque bloc, les moments magnétiques, fortement corrélés, se comportent grossièrement comme un moment magnétique unique. On modifie ensuite la maille du nouveau réseau et la longueur des moments magnétiques jusqu’à revenir à un système analogue au système initial mais dans lequel les interactions sont différentes.

Admettant qu’un tel procédé, appelé renormalisation , conduise à l’existence d’une relation entre les interactions effectives (c’est-à-dire les interactions divisées par la température absolue T) K et K , avant et après transformation, Kadanoff en avait déduit les lois d’échelle ; mais, n’ayant pu obtenir explicitement la forme de la relation K = f (K), il lui avait été impossible de calculer les exposants critiques. Cet auteur avait toutefois montré le résultat important suivant: le point de transition correspond à un point fixe de la transformation f , c’est-à-dire un point K tel que K = f (K), et les exposants critiques sont déterminés par le comportement de f au voisinage du point fixe.

Wilson va beaucoup plus loin. Il prouve tout d’abord que le procédé de Kadanoff ne peut conduire à un résultat correct que dans certaines conditions. C’est le cas, par exemple, si la dimensionalité du système est voisine de 4. Il réussit alors à obtenir les relations qui traduisent la transformation des interactions effectives, appelées équations du groupe de renormalisation, et en déduit un développement des exposants critiques en puissances de 﨎 = 4 漣 d , où d est la dimensionalité du système, valable pour 﨎 礪 0, c’est-à-dire d 麗 4. Ainsi, par exemple, l’exposant 塚 de la susceptibilité isotherme relative au paramètre d’ordre est donné, dans le cas du modèle n -vectoriel, par:

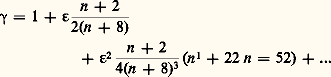À la suite de Wilson, de nombreux travaux ont montré la puissance et la généralité de la méthode. Un nombre important de nouvelles techniques de renormalisation ont été proposées. Citons la méthode de Niejmeijer et Van Leeuwen, dite de renormalisation dans l’espace réel, particulièrement intéressante qui, à côté des grandeurs critiques, permet aussi de déterminer des grandeurs non critiques, par exemple une ligne de transition, c’est-à-dire la manière dont varie la température de transition d’un système lorsqu’on applique un champ extérieur. Ces dernières années, le groupe de renormalisation a été appliqué aux systèmes désordonnés dans lesquels les interactions sont aléatoires, aux systèmes dilués dans lesquels le phénomène de percolation joue un rôle essentiel, aux systèmes semi-infinis dans lesquels les effets de surface ne peuvent pas être négligés...

Le domaine d’applications du groupe de renormalisation s’élargit chaque jour. Ainsi, la suite de nombres réels (x ⁿ ) appartenant à l’intervalle [0, 1], déterminée par la relation de récurrence:

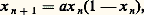se comporte différemment suivant les valeurs du paramètre a. Utilisant le groupe de renormalisation, M. Feigenbaum a montré l’universalité de ce résultat. Celui-ci ne dépend pas, en effet, de la forme explicite de la relation de récurrence. Toute équation de la forme x ^{n + 1} = f (a , x ⁿ ) a les mêmes propriétés si f (a , 0) = f (a , 1) = 0, et s’il existe un seul point c , entre 0 et 1, tel que f (a , c ) = 0. Ces résultats sont d’une grande importance pour ce qu’on appelle le chaos déterministe ^{[cf. CHAOS (physique)]} et trouvent leur application dans la théorie de la turbulence (cf. TURBULENCE).

Encyclopédie Universelle. 2012.